-->
/

Pembahasan Soal ON MIPA PT 2015 Matematika Analisis Kompleks Uraian No 2

Edit
Dibawah ini adalah pembahasan soal analisis kompleks on mipa pt 2015 untuk bidang matematika.
Olimpiade Nasional Matematika dan Ilmu Pengetahuan Alam atau yang biasa disingkat ON MIPA-PT Tahun 2015 telah di selenggarakan dan telah diperoleh pemenang nya. Seleksi ON MIPA Tahun 2015 terdiri dari 4 (empat) bidang yaitu Matematika, Fisika, Kimia, dan Biologi. Bidang Matematika sendiri juga memiliki 5 macam soal seleksi yaitu, Aljabar Linier, Analisis Real, Analisis Kompleks, Kombinatorika, dan Struktur Aljabar.

Pembahasan Soal ON MIPA PT 2015

Jawaban Pembahasan SOAL ON MIPA PT Matematika Analisis Kompleks

Analisis Kompleks Bagian Kedua Uraian

Soal 2. Hitunglah
\displaystyle \int\limits_{0}^{{2\pi }}{{{{e}^{{{{e}^{{2it}}}-3it}}}dt}}
Solusi. Pandang Integral berikut pada C lingkaran dengan jari-jari satu berpusat di titik asal
\displaystyle \oint_{C}{{\frac{{{{e}^{{{{z}^{2}}}}}dz}}{{{{z}^{4}}}}}}
Pada C berlaku 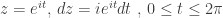z={{e}^{{it}}},\,dz=i{{e}^{{it}}}dt\,\,,\,0\le t\le 2\pi  sehingga integral diatas menjadi
\displaystyle \oint_{C}{{\frac{{{{e}^{{{{z}^{2}}}}}dz}}{{{{z}^{4}}}}}}=\oint_{C}{{\frac{{{{e}^{{{{e}^{{2it}}}}}}i{{e}^{{it}}}dt}}{{{{e}^{{4it}}}}}}}=i\int\limits_{0}^{{2\pi }}{{\frac{{{{e}^{{{{e}^{{2it}}}}}}dt}}{{{{e}^{{3it}}}}}}}=i\int\limits_{0}^{{2\pi }}{{{{e}^{{{{e}^{{2it}}}-3it}}}dt}}
Integral terakhir merupakan bagian yang kita cari. Menurut Cauchy integral
\displaystyle \oint_{C}{{\frac{{{{e}^{{{{z}^{2}}}}}dz}}{{{{z}^{4}}}}}}=\frac{{2\pi i}}{{3!}}\cdot {{\left. {\frac{{{{d}^{3}}({{e}^{{{{z}^{2}}}}})}}{{d{{z}^{3}}}}} \right|}_{{z=0}}}=\frac{{2\pi i}}{{3!}}\cdot 0=0
Jadi integral yang kita cari juga bernilai 0.
Sumber: TheInspires.wordpress.com

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel