Pembahasan Soal ON MIPA PT 2016 Matematika : Analisis Kompleks Bagian Pertama Isian
Dibawah ini adalah pembahasan soal analisis kompleks on mipa pt 2016 utnuk bidang matematika.
Olimpiade Nasional Matematika dan Ilmu Pengetahuan Alam atau yang biasa disingkat ON MIPA-PT Tahun 2016 telah di selenggarakan dan telah diperoleh pemenang nya. Seleksi ON MIPA Tahun 2016 terdiri dari 4 (empat) bidang yaitu Matematika, Fisika, Kimia, dan Biologi. Bidang Matematika sendiri juga memiliki 5 macam soal seleksi yaitu, Aljabar Linier, Analisis Real, Analisis Kompleks, Kombinatorika, dan Struktur Aljabar.
Pembahasan Soal ON MIPA PT 2016
Jawaban Pembahasan SOAL ON MIPA PT Matematika Analisis Kompleks
Bagian I Isian
Soal 1. Hitunglah
Solusi. Dalam bentuk polar persamaan diatas menjadi
Soal 2. Diketahui fungsi  . Selidiki apakah ada fungsi harmonic
. Selidiki apakah ada fungsi harmonic  sehingga
sehingga  analitik. Jika ada, Tuliskan!
analitik. Jika ada, Tuliskan!
Solusi. Ya ada. (Mudah diperiksa bahwa  harmonis)
harmonis)
Dari persamaan Cauchy Riemaan
Integralkan  terhadap
terhadap 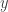 maka
maka
Dimana  adalah fungsi riil sembarang terhada
adalah fungsi riil sembarang terhada 
Ganti 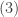 ke dalan
ke dalan  untuk mendapatkan
untuk mendapatkan
atau  dan
dan 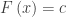 sehingga diperoleh
sehingga diperoleh
Soal 3. Carilah nilai maksimum dari  pada cakram satuan tertutup
pada cakram satuan tertutup  .
.
Soal 4. Tentukan residu di  dari fungsi
dari fungsi
Solusi. Residu di  adalah koefisien
adalah koefisien  pada ekspansi
pada ekspansi
yaitu
Sumber: TheInspires.wordpress.com
