Pembahasan Soal ON MIPA PT 2015 Matematika Kombinatorika
Dibawah ini adalah pembahasan soal kombinatorika on mipa pt 2015 untuk bidang matematika.
Olimpiade Nasional Matematika dan Ilmu Pengetahuan Alam atau yang biasa disingkat ON MIPA-PT Tahun 2015 telah di selenggarakan dan telah diperoleh pemenang nya. Seleksi ON MIPA Tahun 2015 terdiri dari 4 (empat) bidang yaitu Matematika, Fisika, Kimia, dan Biologi. Bidang Matematika sendiri juga memiliki 5 macam soal seleksi yaitu, Aljabar Linier, Analisis Real, Analisis Kompleks, Kombinatorika, dan Struktur Aljabar.
Pembahasan Soal ON MIPA PT 2015
Jawaban Pembahasan SOAL ON MIPA PT Matematika Kombinatorika
Jawaban Kombinatorika
Soal 8. (Bagian I) untuk setiap bilangan asli 
dengan 
, nilai dari
dengan , nilai dari
Adalah…….
Solusi. Misal
Dengan menggunakan sifat kesimetrisan binomial
diperoleh
Jumlahkan 
dan 
untuk memperoleh
dan untuk memperoleh
Jadi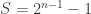 
Soal 3. (Bagian II) misalkan 
adalah sebuah bilangan positif. Buktikan bahwa
adalah sebuah bilangan positif. Buktikan bahwa
Solusi. misal
mudah dilihat bahwa
(ini jelas karena 
)
)Selanjutnya dengan menggunakan substitusi 
diperoleh
diperoleh![\displaystyle \begin{array}{l}{{H}_{n}}=\int\limits_{0}^{1}{{\frac{{1-{{x}^{n}}}}{{1-x}}}}dx\\\,\,\,\,\,\,\,=-\int\limits_{1}^{0}{{\frac{{1-{{{\left( {1-u} \right)}}^{n}}}}{u}}}du\\\,\,\,\,\,\,\,=\int\limits_{0}^{1}{{\frac{{1-{{{\left( {1-u} \right)}}^{n}}}}{u}}}du\\\,\,\,\,\,\,\,=\int\limits_{0}^{1}{{\left[ {\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{u}^{{k-1}}}}}} \right]}}du\\\,\,\,\,\,\,\,=\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}}\int\limits_{0}^{1}{{{{u}^{{k-1}}}}}du\\\,\,\,\,\,\,\,=\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\frac{1}{k}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}}\end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cbegin%7Barray%7D%7Bl%7D%7B%7BH%7D_%7Bn%7D%7D%3D%5Cint%5Climits_%7B0%7D%5E%7B1%7D%7B%7B%5Cfrac%7B%7B1-%7B%7Bx%7D%5E%7Bn%7D%7D%7D%7D%7B%7B1-x%7D%7D%7D%7Ddx%5C%5C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%3D-%5Cint%5Climits_%7B1%7D%5E%7B0%7D%7B%7B%5Cfrac%7B%7B1-%7B%7B%7B%5Cleft%28+%7B1-u%7D+%5Cright%29%7D%7D%5E%7Bn%7D%7D%7D%7D%7Bu%7D%7D%7Ddu%5C%5C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%3D%5Cint%5Climits_%7B0%7D%5E%7B1%7D%7B%7B%5Cfrac%7B%7B1-%7B%7B%7B%5Cleft%28+%7B1-u%7D+%5Cright%29%7D%7D%5E%7Bn%7D%7D%7D%7D%7Bu%7D%7D%7Ddu%5C%5C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%3D%5Cint%5Climits_%7B0%7D%5E%7B1%7D%7B%7B%5Cleft%5B+%7B%5Csum%5Climits_%7B%7Bk%3D1%7D%7D%5E%7Bn%7D%7B%7B%7B%7B%7B%5Cleft%28+%7B-1%7D+%5Cright%29%7D%7D%5E%7B%7Bk-1%7D%7D%7D%5Cleft%28+%7B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D+n+%5C%5C+k+%5Cend%7Barray%7D%7D+%5Cright%29%7B%7Bu%7D%5E%7B%7Bk-1%7D%7D%7D%7D%7D%7D+%5Cright%5D%7D%7Ddu%5C%5C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%3D%5Csum%5Climits_%7B%7Bk%3D1%7D%7D%5E%7Bn%7D%7B%7B%7B%7B%7B%5Cleft%28+%7B-1%7D+%5Cright%29%7D%7D%5E%7B%7Bk-1%7D%7D%7D%5Cleft%28+%7B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D+n+%5C%5C+k+%5Cend%7Barray%7D%7D+%5Cright%29%7D%7D%5Cint%5Climits_%7B0%7D%5E%7B1%7D%7B%7B%7B%7Bu%7D%5E%7B%7Bk-1%7D%7D%7D%7D%7Ddu%5C%5C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%3D%5Csum%5Climits_%7B%7Bk%3D1%7D%7D%5E%7Bn%7D%7B%7B%7B%7B%7B%5Cleft%28+%7B-1%7D+%5Cright%29%7D%7D%5E%7B%7Bk-1%7D%7D%7D%5Cfrac%7B1%7D%7Bk%7D%5Cleft%28+%7B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D+n+%5C%5C+k+%5Cend%7Barray%7D%7D+%5Cright%29%7D%7D%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0 "\displaystyle \begin{array}{l}{{H}_{n}}=\int\limits_{0}^{1}{{\frac{{1-{{x}^{n}}}}{{1-x}}}}dx\\\,\,\,\,\,\,\,=-\int\limits_{1}^{0}{{\frac{{1-{{{\left( {1-u} \right)}}^{n}}}}{u}}}du\\\,\,\,\,\,\,\,=\int\limits_{0}^{1}{{\frac{{1-{{{\left( {1-u} \right)}}^{n}}}}{u}}}du\\\,\,\,\,\,\,\,=\int\limits_{0}^{1}{{\left[ {\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{u}^{{k-1}}}}}} \right]}}du\\\,\,\,\,\,\,\,=\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}}\int\limits_{0}^{1}{{{{u}^{{k-1}}}}}du\\\,\,\,\,\,\,\,=\sum\limits_{{k=1}}^{n}{{{{{\left( {-1} \right)}}^{{k-1}}}\frac{1}{k}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}}\end{array}")
Sumber: TheInspires.wordpress.com